Mnemonics are useless
In the age of the internet, the mnemonic is a relic from a bygone era.
I’ve never really understood the urge people get to try and learn Japanese after they get sufficiently into anime. I imagine this comes across as hypocritical from someone who’s been studying the language a good year for the sole reason of understanding Vtubers, but back when I was just into anime, it never even crossed my mind to attempt to learn Japanese. It seemed like a utterly unnecessary exercise: all the Japanese media I consumed at the time invariably had translations, and I had a vague enough idea of the difficulty in learning another language that doing it for the clout was way too much effort. I guess that’s the part a lot of people somehow miss: language learning is ridiculously hard if you don’t have the sufficient motivation or circumstance.
All my friends who started learning Japanese after I did tapped out pretty quickly. Flimsy motivations notwithstanding, they also tapped out at the first real challenge in the entire process: cramming hundreds of words into your head as a baseline before you actually start immersing in the language. While I imagine this process is universal across all languages, Japanese also has the additional issue of the Kanji (漢字) system.
Japanese has two syllabaries: Hiragana (ひらがな) and Katakana (カタカナ). They’re pretty simple: 46 characters each, and they’re used to write out the sounds of the language. Hiragana is used for native Japanese words, and Katakana is used for foreign words. Kanji are the 10 thousand or so Chinese characters that form the third fundamental part of the Japanese writing system. They’re a necessary evil: a lack of word boundaries means you can’t read the language otherwise, and even if you put in spaces between words completely written in Hiragana,
Learning Kanji is an arduous task, and as such there have been a lot of debate in the community as to the most efficient way to cram in these initially inexplicable moonrunes. One common way is to build it up from raw materials: kanji generally are made of radicals, and the meaning of each kanji is sometimes associated with the radicals it’s made of. A natural extension of this, and the method I used initially, is the Remembering The Kanji (RTK) method.
The RTK Method associates each Kanji with a mnemonic based on the radicals
That doesn’t happen.
It just doesn’t.
Mnemonics are a practically unnecessary crutch
Say you hit a Kanji which you don’t immediately recognize, but which you’ve “learnt” via the RTK method. You now have to pause reading, remember the mnemonic, go through it in your head
This is my core issue with mnemonics. They’re a crutch that’s functionally unnecessary if you’re actually going to be using the information you’re trying to remember. Recall is only useful if it’s fast. Slow recall may as well be equivalent to not knowing the information at all, because guess what? We all have the Library of Babel in our pockets. We have the All-Knowning Information Box just sitting there, and we all have the muscle memory to look things up faster than we could spit out the damn mnemonic.
The only time mnemonics are useful is when you’re in an environment where you can’t look things up, and it’s sort of fine to take your time to remember it. I posit that most of these environments are either contrived or outdated: the most egregious offender being exams. They should be open book anyway if you actually want to test the material in any rigorous fashion; If your exam can be aced if you have your notes with you, then it isn’t a very good exam to begin with. The only other situations I can think of is something like surgery, where you might not have the luxury of whipping out your phone during someone’s heart transplant, but could spare the seconds to mnemonic out the rib bones or whatever. Still, I don’t know about you but I definitely wouldn’t want my surgeon to be relying on a mnemonic to remember where the liver is.
Mnemonics replace understanding
In some cases, you shouldn’t be memorizing at all. Once you actually understand the topic, whatever you’re trying to remember becomes trivial as you figure out the underlying structure. Education that focuses on memorization over understanding is doomed to fail.
As someone who went to school in India, this is a reoccurring cliche across basically every single subject. But even for educational systems that aren’t utter dogshit, there still exists remnants. Mnemonics are a notable canary in the coal mine.
Let’s take trignometry. Two well-known mnemonics here: SOH-CAH-TOA and All Students Take Calculus.
SOH-CAH-TOA
A nice clean mnemonic for remembering how the basic trigonometric functions relate to the sides of a triangle:
Sine = Opposite ÷ Hypotenuse
Cosine = Adjacent ÷ Hypotenuse
Tangent = Opposite ÷ Adjacent
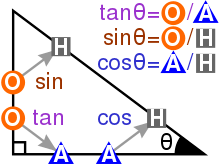
Now, this one is bad on the face of it. Trigonometry is used so consistently in your school education that needing a mnemonic to remember this is unnecessary by itself. However, this framing also fundamentally misunderstands the trigonometric functions. They are not about triangles, they’re about circles.
Indeed, the only reason we usually care about the trigonometric functions is because for a particular point on the circle, its coordinates \((x, y)\) is \((\cosθ,\sinθ)\).
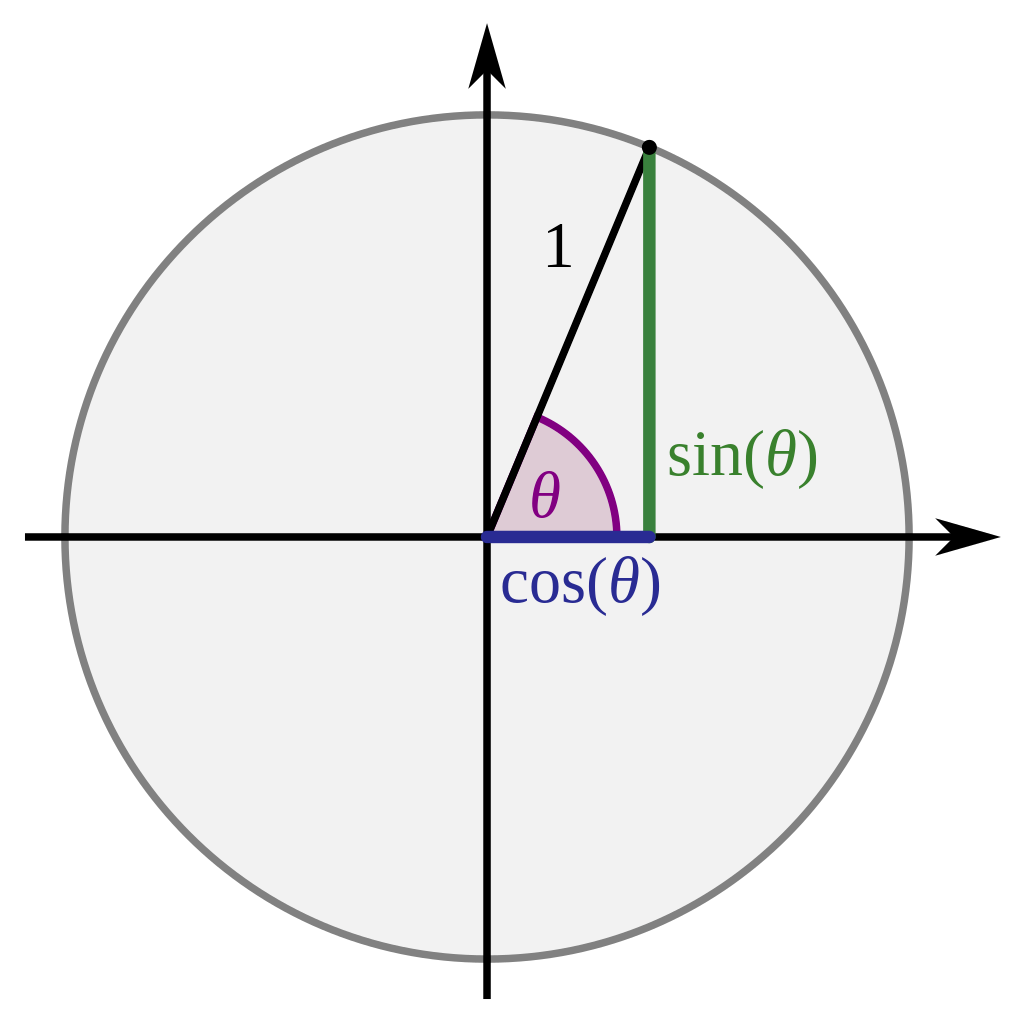
It is in this context where trigonometry is actually useful. This perspective is the fundamental to further understanding down the line as trigonometry pops up again and again in different contexts. 3Blue1Brown makes this point way better than I can in this video where he teaches trigonometry fundamentals, so give that a watch.
Now, while \(\sin\) and \(\cos\) are the main two, all trigonometric functions are indeed foundationally mapped on the circle:
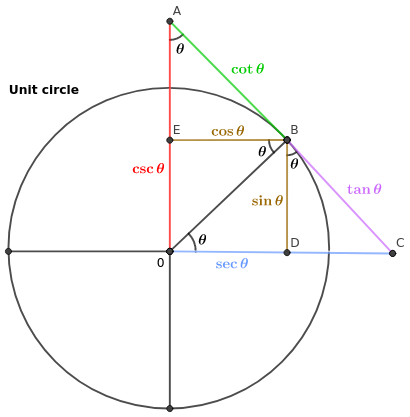
\(\cot\), \(\csc\) and \(\cot\) are for the most part remnants of an era where math’s most practical application was marine navigation. \(\tan\) is, well, the tangent, so being the length of the tangent where it intersects the x-axis makes sense. Practically, you don’t even need to remember what it represents, just how it relates to \(\sin\) and \(\cos\).
What you’re left to memorize then is that \(\sin\theta\) is \(y\), \(\cos\theta\) is \(x\), and \(\tan\) is \(\frac{\sin\theta}{\cos\theta}\). For circles of a non-unit radius \(r\), the functions would scale too. Considering \(r\) is actually the hypotenuse of the triangle in question, one can derive pretty easily the relations with the sides.
Now, you might complain that this isn’t that big of a reduction in memory. Indeed, with the mnemonic, it’s true that the original is probably easier to immediately cram into your head. However the original perspective is antithetical to an actual understanding of what you’re doing, and makes things harder later down the line. Case in point: the quadrants.
All Students Take Calculus (or any of its million variations)
The Cartesian plane can be subdivided into quadrants depending on the sign of the axis, and in each quadrant the signs of the trigonometric functions vary:
- Quadrant I (angles from 0 to 90 degrees, or 0 to π/2 radians): All trigonometric functions are positive in this quadrant.
- Quadrant II (angles from 90 to 180 degrees, or π/2 to π radians): Sine and cosecant functions are positive in this quadrant.
- Quadrant III (angles from 180 to 270 degrees, or π to 3π/2 radians): Tangent and cotangent functions are positive in this quadrant.
- Quadrant IV (angles from 270 to 360 degrees, or 3π/2 to 2π radians): Cosine and secant functions are positive in this quadrant. The following image uses All Science Teachers (are) Crazy but the concept is the same:

An innocuous tool to memorize mathematical facts, one might say. After all, how would one remember the signs of each trigonometric functions given their angle otherwise? Maybe, I don’t know, looking at where it is on the fucking circle.
The signs of \(x\) and \(y\), the defining feature of each quadrant directly give you the signs of \(\sin\) and \(\cos\), and deriving the sign of the rest of the trigonometric functions still takes less time than reciting that dumbass mnemonic.
Many of the conversions in trigonometry become intuitive and quick when this understanding kicks in. Why is \(\sin\theta = -\sin(2\pi - \theta)\)? Just look at the circle! \(\sin\theta = \cos(\frac{\pi}{2} - \theta)\)? Keep in mind the axes, and summon the circle! Want to visualize the function? Rotate around the goddamn circle!
It’s frankly a disgrace: students are given a dumb mnemonic that both robs proper learning and makes things harder to remember in the end. While the mnemonic itself is not necessarily the root of the problem, it’s indicative of a fundamentally incurious form of learning; one that would rather memorize than understand. That’s just sad. Nobody should have to remember All Students Take Calculus.
Final Notes
I imagine a lot of the members in the Memorization community will have several qualms about the opinions I’ve expressed here. So I’ll temper my piece with this: mnemonics are good at what they’re designed to do. They are uniquely effective in letting you memorize (given leeway in terms of recall time) unconnected, disjointed information in large quantities. There’s a reason why literally every memory sports champion uses some form of mnemonics, and it’s the ideal way of learning e.g. the digits of \(\pi\), for instance. I’ll give that to you, mnemonics: you work. I just don’t think you’re very useful.